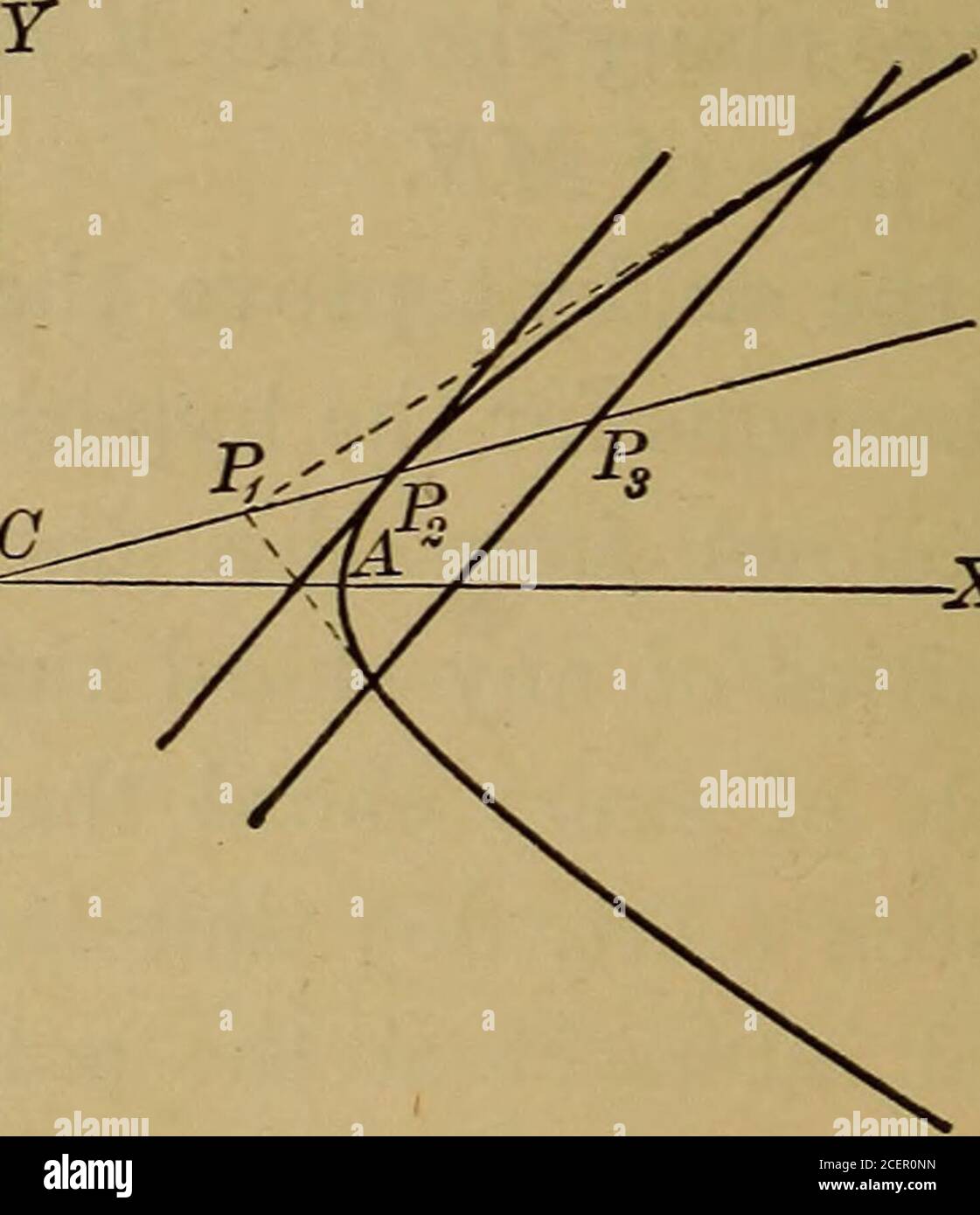
. Géométrie analytique plane et solide ; manuel élémentaire. —X 9 Fig. 88. CH. XII, | PÔLES ET POLAIRES 161 Laissez les coordonnées du point P2 où CPX coupe l'hyperbole être (xvy^). Ensuite, l'équation de la tangente 2 b2x2x — a2y2y = a2b et l'équation du polaire de P1 isb2xxx — A2yxy = a2b2.mais puisque PX et P2 sont sur la même ligne à travers l'origine, -i = -?, et ces lignes sont évidemment parallèles.Laissez l'étudiant prouver le même théorème pour l'ellipse.3. Le polaire de n'importe quel point PX par rapport à une parabole isparallèle à la tangente au point ivhere un diamètre de tout au long de P1 coupe la parabole
RMID:ID de l’image:2CER0NN
Détails de l'image
Contributeur:
Reading Room 2020ID de l’image:
2CER0NNTaille du fichier:
7,1 MB (138,1 KB Téléchargement compressé)Autorisations:
Modèle - non | Propriété - nonUne autorisation est-elle nécessaire?Dimensions:
1468 x 1702 px | 24,9 x 28,8 cm | 9,8 x 11,3 inches | 150dpiInformations supplémentaires:
Cette image appartient au domaine public, ce qui signifie que le droit d’auteur a expiré ou que le titulaire du droit d’auteur a renoncé à ses droits. Les frais facturés par Alamy couvrent l’accès à la copie haute résolution de l’image.
Cette image peut avoir des imperfections car il s’agit d’une image historique ou de reportage.